

Next: Concentration field method
Up: Methods
Previous: Methods
Calculations are performed on a longitude-latitude grid which covers the
spatial domain of interest. We assume that a species emitted within a
grid cell is swept into the air parcel and transported to the receptor
site without loss through diffusion, chemical transformation or
atmospheric scavenging (Cheng et al., 1993). Let 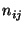 be the total
number of trajectory segment endpoints falling in the grid cell
be the total
number of trajectory segment endpoints falling in the grid cell 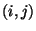 over the
period of study, and let
over the
period of study, and let 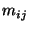 be the number of endpoints in
be the number of endpoints in 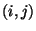 corresponding to trajectories associated with concentration values at
the receptor site exceeding a specified threshold. The ratio
corresponding to trajectories associated with concentration values at
the receptor site exceeding a specified threshold. The ratio
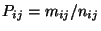 (PSCF) is then the conditional probability that an air
parcel passing over the cell
(PSCF) is then the conditional probability that an air
parcel passing over the cell 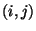 on its way to the receptor site
arrives at the site with concentration values above the threshold.
Hence, high values in the spatial distribution of
on its way to the receptor site
arrives at the site with concentration values above the threshold.
Hence, high values in the spatial distribution of 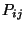 will pinpoint
geographical regions that are likely to produce high concentration
values at the receptor site if crossed by a trajectory.
will pinpoint
geographical regions that are likely to produce high concentration
values at the receptor site if crossed by a trajectory.
In order to identify the high PSCF values that might have arisen purely
by chance, it is necessary to test these values against the null
hypothesis that there is no association between concentrations and
trajectories (Vasconcelos et al., 1996b). The statistical significance of
the spatial distribution of the PSCF values is examined by making use of
a nonparametric bootstrap method (Wehrens et al., 2000). The method assumes
that the concentration values are independent and identically
distributed. We draw with replacement from the original concentration
data set, 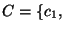
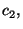
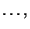
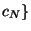 ,
, 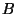 random subsamples of size equal to
the length of the data set,
random subsamples of size equal to
the length of the data set,
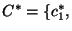
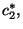
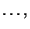
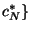 . We then calculate for each bootstrapped sample
. We then calculate for each bootstrapped sample 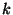 the
corresponding PSCF spatial distribution,
the
corresponding PSCF spatial distribution, 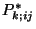 . Let
. Let
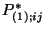
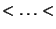
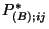 be the ordered values
be the ordered values
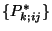 ,
,
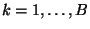 , and let
, and let 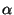 be the chosen
significance level. If
be the chosen
significance level. If
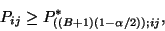 |
(1) |
the null hypothesis is rejected at
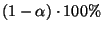 confidence level. We decide to retain for our
further analysis only the PSCF values satisfying the above relation.
Note that if there are more than one trajectory assigned to a concentration
value, the simple bootstrap on the concentration data set is equivalent
to a blocked bootstrap on the trajectory set.
confidence level. We decide to retain for our
further analysis only the PSCF values satisfying the above relation.
Note that if there are more than one trajectory assigned to a concentration
value, the simple bootstrap on the concentration data set is equivalent
to a blocked bootstrap on the trajectory set.


Next: Concentration field method
Up: Methods
Previous: Methods
Alexandru Lupu
2002-08-20
![]()
![]()
![]()
![]() ,
, ![]() random subsamples of size equal to
the length of the data set,
random subsamples of size equal to
the length of the data set,
![]()
![]()
![]()
![]() . We then calculate for each bootstrapped sample
. We then calculate for each bootstrapped sample ![]() the
corresponding PSCF spatial distribution,
the
corresponding PSCF spatial distribution, ![]() . Let
. Let
![]()
![]()
![]() be the ordered values
be the ordered values
![]() ,
,
![]() , and let
, and let ![]() be the chosen
significance level. If
be the chosen
significance level. If