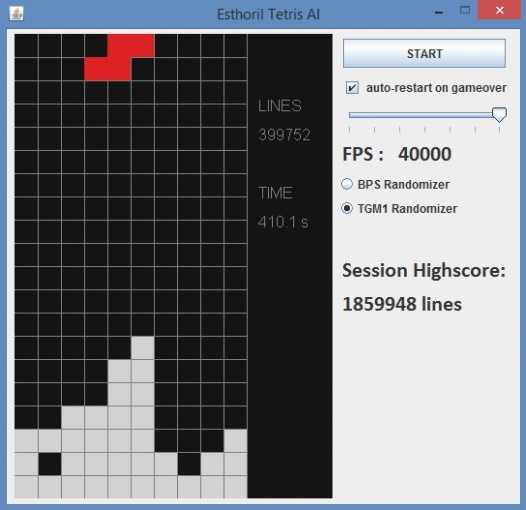
An algorithm trained with genetic evolution to play the most iconic video game ever. Scroll down to see how it works. I had a Java clone lying around for some time when I found out the Bizhawk emulator let's you run LUA scripts so did some research, ported the script and let it run wild.
A bit of Tetris history. Once you reach lvl 30, you enter the so-called kill screen. The blocks double their speed, moving down one line per frame making it unable for humans to succesfully continue playing. With expert play, you can hit 999.999 just before reaching the kill screen. This was done as a safeguard to prevent the game from crashing.
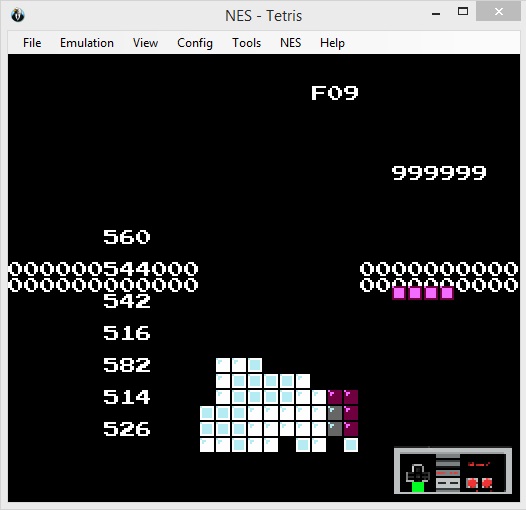
In the 8-bit era, memory was limited and a fixed amount of memory was allocated to store variables. For example, the number to keep track of the level uses 5 bits (11111 being 31). If the level would become higher, other bits of memory are overwritten. Bits that might store information for something else. This results in the unusual colour schemes in the second and third picture and the game eventually crashing. So make sure humans can't get that far and you're good. Smart. This limitation gets circumvented by the LUA script, which just keeps smashing buttons until the game eventually crashes after completing around 1500 lines.
You can find an unedited 17 minute video on YouTube of it playing NES Tetris to 999.999. Better than watching paint dry but not much.
Java desktop application at 400K lines cleared
Maxed out NES Tetris
Game crashes just over 1500 linesLet's define a heuristic function to figure out where to place a new piece. when we get a new piece, our function calculates a score from several properties of our playing field. Just think logically about how you would play Tetris and what is important to do well. Making lines, having no holes in your playing field, the top being smooth rather than very bumpy. And write a few little functions to measure these metrics.
| Landing height | Number of rows the piece can move down |
| Lines cleared | Number of lines cleared |
| Row transitions | Number of times we go from an empty square to a filled square or vice versa in each row |
| Column transitions | Same but for columns |
| Holes | Number of cells with a filled square above |
| Wells | Number of stacked empty squares |
| Board height | Total height of all columns |
For example, given this next piece and board state
we calculate the score with our heuristic function for all possibile positions and orientations of this piece and keep track of the best result. The position and orientation yielding the best score is where we put the piece. In our example, the case with red border.
Doesn't sound too bad. Unfortunately just this won't perform all that well, as not every metric in our heuristic is equally important. We assign weights to them. But what value to give these weight?
Score = a x (landing height) + b x (lines cleared) + c x (row transitions) + ...
Insert genetic evolution to determine our weights a, b, c, .... Short explanation. We create a first generation of 1000 individuals with random weights. We let them all play a bunch of Tetris and keep track of their highscores. The individuals performing best will become the parents of our next generation. Take a few weights from both parents and you have a child. Add a small chance for randomness because we don't want inbreeding. Replace the worst performers with our new children and we have our next generation. Repeat until you are destroying Tetris.
First I made a Java version capable of clearing millions of lines. Then I ported it to LUA so I could run it on the BizHawk emulator playing actual 8bit NES Tetris. This RAM map made life easier, being able to read the gamestate directly from memory. That's all.