Fourier-reeksen
Deze worksheet sluit aan bij paragraaf 3.2 op pagina 15 e.v.
restart;
assume(n,integer);
with(plots):
Warning, the name changecoords has been redefined
Iedere lijn definieert een functie en de corresponderende periode. Kies er een uit door het # symbool te verwijderen.
#f:=x->x+Pi; L:=Pi;
#f:=x->piecewise(x <0,x+Pi,Pi-x); L:=Pi;
f:=x->piecewise(abs(x) <1,1,0); L:=2;
#f:=x->piecewise(x<0,1,-1); L:=Pi;
#f:=x->piecewise(abs(x)<Pi/2,sin(x),0); L:=Pi;
#f:=x->abs(sin(x)); L:=Pi;
plot(f(x),x=-L..L);
teken de functie
aantaltermen:=20:
definieer het aantaltermen dat je hoogstens zal tonen
![]()
![]()
![[Maple Plot]](images/fourier3.gif)
De formules van Euler
a[0]:='1/(2*L)*int( f(x),x=-L..L)'=1/(2*L)*int(f(x),x=-L..L);
a[0]:=1/(2*L)*int(f(x),x=-L..L):
a[n]:='1/(L)*int(f(x)*cos(n*x*Pi/L),x=-L..L)'=1/L*int(f(x)*cos(n*x*Pi/L),x=-L..L);
a[n]:=1/L*int(f(x)*cos(n*x*Pi/L),x=-L..L):
b[n]:='1/(L)*int(f(x)*sin(n*x*Pi/L),x=-L..L)'=1/L*int(f(x)*sin(n*x*Pi/L),x=-L..L);
b[n]:=1/L*int(f(x)*sin(n*x*Pi/L),x=-L..L):
![a[0] := 1/2/L*int(f(x),x = -L .. L) = 1/2](images/fourier4.gif)
![a[n] := 1/L*int(f(x)*cos(n*x*Pi/L),x = -L .. L) = 2...](images/fourier5.gif)
![b[n] := 1/L*int(f(x)*sin(n*x*Pi/L),x = -L .. L) = 0...](images/fourier6.gif)
Hier wordt een benadering met N termen gedefinieerd. benadering:=N->a[0]+sum(a[n]*cos(n*Pi*x/L)+b[n]*sin(n*Pi*x/L),n=1..N);
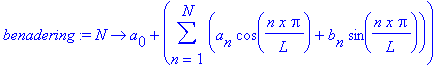
Wil je de formule voor een zekere benadering zien ? Je kunt de benadering ook vergelijken met de functie zelf
benadering(7);
plot({benadering(7),f(x)},x=-L..L,discont=true);
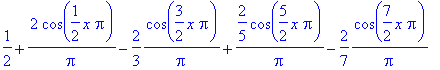
![[Maple Plot]](images/fourier9.gif)
Je kunt de opeenvolgende benaderingen tonen met een animatie. animate({f(x),benadering(nr)},x=-L..L,nr=0..aantaltermen);
![[Maple Plot]](images/fourier10.gif)
Hoe goed is de benadering ? De fout moet dalen naarmate het aantal termen in de benadering toeneemt.
for k from 1 to aantaltermen do
err[k]:=evalf(integrate((f(x)-benadering(k))^2,x=-L..L)) ;
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>