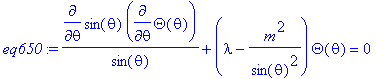
Oplossing voor de kwantummechanische behandeling
van het draaimoment van de baanbeweging
Deze oplossing sluit aan bij paragraaf 6.4.2 op pagina 102 e.v.
.
We starten met de definitie van het probleem, namelijk de vergelijking (6.50).
>
restart;
Herstart Maple. Alle vorige berekeningen gaan verloren.
eq650 := '1/sin(theta)*diff(sin(theta)*diff(Theta(theta),theta),theta)
+(lambda-m^2/sin(theta)^2)*Theta(theta)=0';
diff(f(x),x$n) is de n'de afgeleide naar x van f(x)
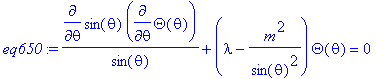
We voeren een eerste substitutie door en bekomen de vergelijking in v(u).
>
with(DEtools):
Dchangevar(theta=arccos(u),Theta(theta)=v(u),eq650,theta,u);
eq651:=collect(%,[v,diff(v(u),u),diff(v(u),u$2)],simplify);
>
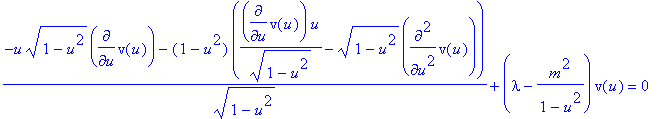
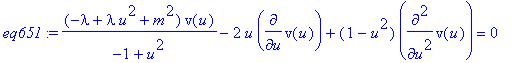
Van de bovenstaande vergelijking zoeken we een oplossing in de vorm van een reeksontwikkeling.
>
with(powseries):
F51 := powsolve(factor(eq651*(u^2-1))) :
noem de oplossing van eq551 F51
F51(_k);
we vinden een 3-terms recursie
![]()
![]()
We bekwamen dus een recursiebetrekking in 3 termen. We kunnen een betrekking in 2 termen bekomen door nog een substitutie door te voeren :
>
v:=u->(1-u^2)^(abs(m)/2)*y(u);
simplify(eq651/(1-u^2)^(abs(m)/2),[m^2=abs(m)^2]);
eq652:=unapply( collect(%,[diff(y(u),u$2),diff(y(u),u),y(u)],simplify) ,m);
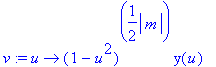
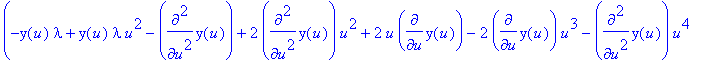
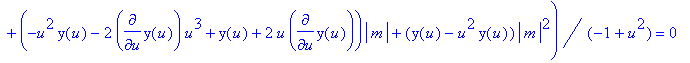
![]()
Van de bovenstaande vergelijking zoeken we opnieuw een oplossing in de vorm van een reeksontwikkeling.
> F52 := powsolve(eq652(m)) : noem de oplossing F52
> F52a := tpsform(F52,x,10); F52a toont deze reeksontwikkeling uitgewerkt tot de 10'de macht
![]()
![]()
![]()
![]()
![]()
> collect(convert(F52a,polynom),[C0,C1,x],factor); converteer F52a eerst naar een veelterm; orden de termen eerst volgens machten van C0, vervolgens machten van C1 en hierbinnen in machten van x. De machten van x moeten ontbonden worden in factoren.
![]()
![]()
![]()
![]()
![]()
![]()
> F52(_k); F52 is een reeksontwikkeling met F52(_k)=a_k als coefficient van x^k
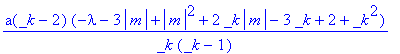
> subs(_k=n+2,F52(_k)/F52(_k-2)); vervang _k door n+2 en we bekomen een recursiebetrekking
> collect(%,lambda,factor); vereenvoudig deze uitdrukking
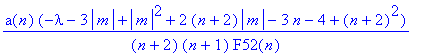
![]()
>
factor(solve(%=0,lambda));
los deze vergelijking op naar lambda
subs({lambda=l*(l+1)},%%);
dit is de nieuwe uitdrukking voor a(n+2)
![]()
![]()
Ben je alleen geinteresseerd in de oplossing en niet zozeer in de recursiebetrekking, dan kan dit ook als volgt :
>
dsolve(eq652(m),y(u),type=series);
los (6.52) op naar y(x) in de vorm van een reeksontwikkeling
subs({y(0)=C0,D(y)(0)=C1},collect(%,u,factor));
vervang y(0) en y'(0) door constanten C0 en C1, groepeer volgens machten van x en ontbind deze coefficienten in factoren. Je bekomt dezelfde oplossing als F47a.
![]()
![]()
![]()
![]()
![]()
![]()
Nu we de algemene vorm kennen, kunnen we voor een gegeven koppel (l,m) de eigenfunctie bepalen. Dit gebeurt in de volgende procedure.
>
Theta := proc(l,m,x)
local expr, hulp, reeks, polyn, C, t, sol;
sol := powsolve(eq652(m)):
reeks:=tpsform(sol,t,l-abs(m)+1);
bepaal de reeks
polyn:=convert(reeks,polynom);
maak er een veelterm van
if type(l-abs(m),even) then
de ene reeks wordt afgebroken en de andere verdwijnt
hulp:=subs({C0=C,C1=0,lambda=l*(l+1)},polyn)
else hulp:=subs({C0=0,C1=C,lambda=l*(l+1)},polyn);
fi;
expr:=sin(x)^(abs(m))*subs(t=cos(x),hulp);
vermenigvuldig met de sin(theta)^|m| en substitueer t=cos(x)
simplify(integrate(sin(x)*expr^2,x=0..Pi));
bepaal de overblijvende constante
solve(%=1,C);
hier krijg je de mogelijke c-waarden
RETURN(simplify(subs(C=%[1],expr)));
neem de eerste c-waarde
end:
Hier wordt de bovenstaande procedure gebruikt voor de waarde l=2,m=0
>
t:=Theta(2,0,x);
bepaal de eigenfunctie corresponderend met l=2,m=0
plot( t , x=0..Pi);
teken deze functie
plot( t^2 , x=0..Pi);
teken de waarschijnlijkheidsdichtheid
![]()
![[Maple Plot]](images/draai233.gif)
![[Maple Plot]](images/draai234.gif)
De golffuncties zijn volgens opmerking 6.4.2 veelvouden van de geassocieerde functies van Legendre. Je kan dit hier nagaan.
>
with(orthopoly):
roep een pakket op; P(l,t) is de l-de graads Legendre veelterm
Pa:=proc(l,m,x)
local t,d;
if m=0 then d:=P(l,t) else d:=diff(P(l,t),t$m) fi;
d:=sqrt(1-x^2)^m*subs(t=x,d);
RETURN(simplify(d,trig));
end:
ThetaP:=(l,m,theta)->sqrt((l+1/2)*(l-abs(m))!/(l+abs(m))!)*Pa(l,abs(m),cos(theta));
definitie volgens opmerking 6.4.2
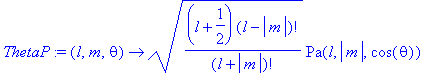
> Theta(3,1,theta);ThetaP(3,1,theta);
![]()
![]()
Vergelijk de twee werkwijzen. Let wel op : er kan een faseverschil optreden tussen de twee resultaten.
>
simplify(Theta(3,1,theta)/ThetaP(3,1,theta),trig);
vereenvoudig een verhouding om een constante over te houden
simplify(abs(%));
de modulus van deze constante is altijd 1
plot({Theta(3,1,theta),ThetaP(3,1,theta)},theta=0..Pi);
>
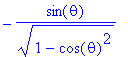
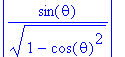
![[Maple Plot]](images/draai240.gif)
Tot slot kunnen we de volledige oplossing construeren (zie voorbeeld 6.4.2. op pagina 104)
> Y:=(l,m,theta,phi)->simplify(1/sqrt(2*Pi)*Theta(l,m,theta))*exp(I*m*phi);
![]()
> Y(2,0,theta,phi);